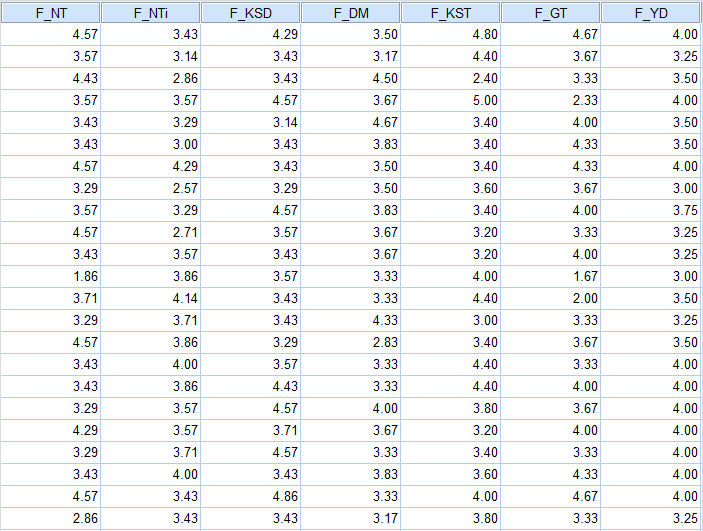
- Biến độc lập: F_NT, F_NTi, F_KSD, F_DM, F_KST, F_GT
- Biến phụ thuộc: F_YD
1. Bảng Model Summary
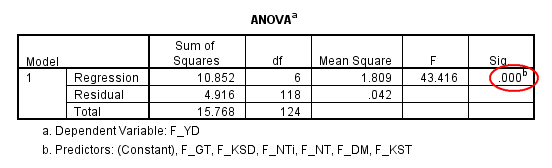
Tổng thể rất lớn, chúng ta không thể khảo sát hết toàn bộ, nên thường trong nghiên cứu, chúng ta chỉ chọn ra một lượng mẫu giới hạn để tiến hành điều tra, từ đó suy ra tính chất chung của tổng thể. Mục đích của kiểm định F trong bảng ANOVA chính là để kiểm tra xem mô hình hồi quy tuyến tính này có suy rộng và áp dụng được cho tổng thể hay không.
Cụ thể trong trường hợp này, giá trị sig của kiểm định F là 0.000 < 0.05. Như vậy, mô hình hồi quy tuyến tính xây dựng được phù hợp với tổng thể.
3. Bảng Coefficients
Trước khi đi vào tìm hiểu các giá trị trong bảng này, mình sẽ nói một ít về thắc mắc của khá nhiều bạn: Sử dụng hệ số hồi quy nào mới là đúng, chuẩn hóa hay chưa chuẩn hóa? Sao lại có bài dùng phương trình hồi quy chuẩn hóa, bài lại dùng hồi quy chưa chuẩn hóa? Có giảng viên yêu cầu viết phương trình chuẩn hóa, giảng viên lại buộc viết phương trình chưa chuẩn hóa?
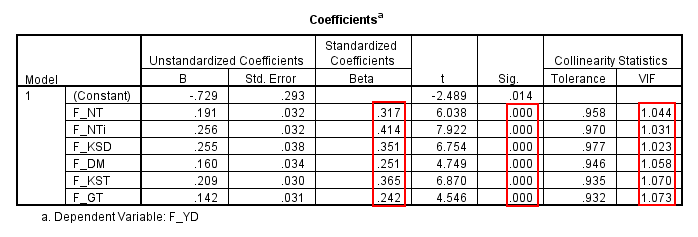
Với dạng đề tài nghiên cứu có mô hình + bảng câu hỏi sử dụng thang đo Likert + chạy phân tích định lượng SPSS thì các bạn nên sử dụng phương trình hồi quy chuẩn hóa, lý do tại sao thì mình vừa dẫn bài viết cho các bạn đọc ngay ở trên rồi. Như vậy, bảng Coefficients, những mục các bạn cần lưu ý gồm cột Hệ số hồi quy chuẩn hóa Beta, cột giá trị Sig, cột VIF.
Đầu tiên là giá trị Sig kiểm định t từng biến độc lập, sig nhỏ hơn hoặc bằng 0.05 có nghĩa là biến đó có ý nghĩa trong mô hình, ngược lại sig lớn hơn 0.05, biến độc lập đó cần được loại bỏ.
Tiếp theo là hệ số hồi quy chuẩn hóa Beta, trong tất cả các hệ số hồi quy, biến độc lập nào có Beta lớn nhất thì biến đó ảnh hưởng nhiều nhất đến sự thay đổi của biến phụ thuộc. Do đó khi đề xuất giải pháp, các bạn nên chú trọng nhiều vào các nhân tố có Beta lớn.
Cuối cùng là VIF, giá trị này dùng để kiểm tra hiện tượng đa cộng tuyến. Theo lý thuyết nhiều tài liệu viết, VIF < 10 sẽ không có hiện tượng đa cộng tuyến. Tuy nhiên trên thực tế với các đề tài nghiên cứu có mô hình + bảng câu hỏi sử dụng thang đo Likert thì VIF < 2 sẽ không có đa cộng tuyến, trường hợp hệ số này lớn hơn hoặc bằng 2, khả năng cao đang có sự đa cộng tuyến giữa các biến độc lập.
Với dữ liệu mình đang chạy, như các bạn thấy sig hệ số hồi quy của các biến độc lập đều nhỏ hơn hoặc bằng 0.05, do đó các biến độc lập này đều có ý nghĩa giải thích cho biến phụ thuộc, không biến nào bị loại bỏ. Hệ số VIF nhỏ hơn 2 do vậy không có đa cộng tuyến xảy ra.
Riêng cột Tolerance, các bạn sẽ thấy một số bài nghiên cứu, tài liệu sử dụng hệ số này để kiểm tra đa cộng tuyến. Nhưng ở đây mình không dùng, bởi vì hệ số này là nghịch đảo của VIF, nên các bạn có thể sử dụng 1 trong 2, cái nào cũng được, thường mọi người hay dùng VIF hơn.
Như vậy phương trình hồi quy chuẩn hóa sẽ là:
XEM VIDEO CHI TIẾT
4. Biểu đồ tần số phần dư chuẩn hóa Histogram
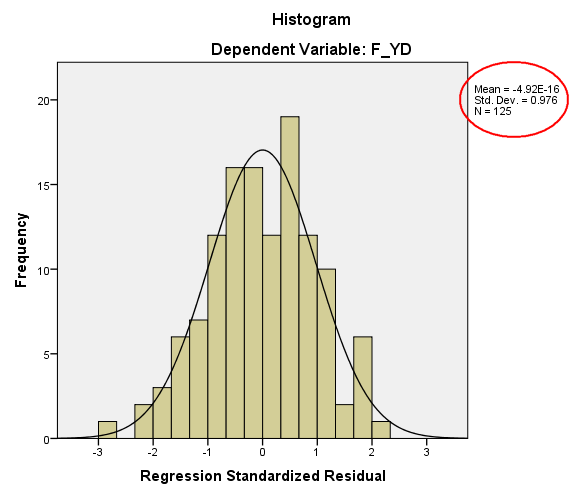
Từ biểu đồ ta thấy được, một đường cong phân phối chuẩn được đặt chồng lên biểu đồ tần số. Đường cong này có dạng hình chuông, phù hợp với dạng đồ thị của phân phối chuẩn. Giá trị trung bình Mean gần bằng 0, độ lệch chuẩn là 0.976 gần bằng 1, như vậy có thể nói, phân phối phần dư xấp xỉ chuẩn. Do đó, có thể kết luận rằng: Giả thiết phân phối chuẩn của phần dư không bị vi phạm.
5. Biểu đồ phần dư chuẩn hóa Normal P-P Plot
Như mình đã đề cập ở mục 4, ngoài cách kiểm tra bằng biểu đồ Histogram, thì P-P Plot cũng là một dạng biểu đồ được sử dụng phổ biến giúp nhận diện sự vi phạm giả định phần dư chuẩn hóa.
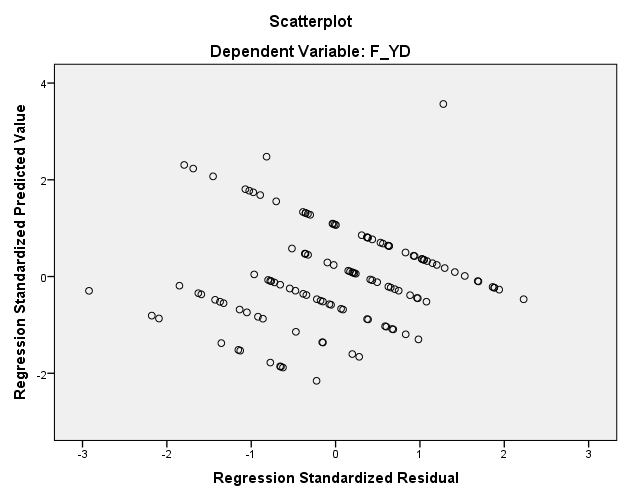
6. Biểu đồ Scatter Plot kiểm tra giả định liên hệ tuyến tính
——–

DienDan.Edu.Vn Cám ơn bạn đã quan tâm và rất vui vì bài viết đã đem lại thông tin hữu ích cho bạn.DienDan.Edu.Vn! là một website với tiêu chí chia sẻ thông tin,... Bạn có thể nhận xét, bổ sung hay yêu cầu hướng dẫn liên quan đến bài viết. Vậy nên đề nghị các bạn cũng không quảng cáo trong comment này ngoại trừ trong chính phần tên của bạn.Cám ơn.