T-Test là một cách để quyết định xem có sự khác biệt nào về độ tin cậy mang tính thống kê (statistically significant) giữa các bộ dữ liệu hay không, sử dụng phân phối t Student. T-Test trong Excel là so sánh giá trị bình quân của hai mẫu. Bài viết này giải thích ý nghĩa thống kê (statistical significance) tức là gì và chỉ ra cách thực hiện T-Test trong Excel.
Lưu ý: Hướng dẫn trong bài viết này áp dụng cho Excel 2019, 2016, 2013, 2010, 2007; Excel for Office 365 và Excel Online.
Ý nghĩa thống kê (statistical significance) là gì?
Giả sử bạn muốn biết con xúc xắc nào trong hai con sẽ cho điểm cao hơn. Bạn lăn con xúc xắc đầu tiên và nhận được 2 điểm. Sau đó, bạn lăn con xúc xắc thứ 2 và nhận được 6 điểm. Điều này có cho bạn biết con xúc xắc thứ hai thường cho điểm cao hơn không? Nếu câu trả lời của bạn “tất nhiên là không”, thì bạn đã có một số hiểu biết nhất định về ý nghĩa thống kê. Bạn hiểu sự khác biệt là do sự thay đổi ngẫu nhiên về điểm số mỗi lần một con xúc xắc được lăn. Vì mẫu rất nhỏ (chỉ có 1 lần lăn xúc xắc) nên nó không cho thấy gì đáng kể.
Bây giờ hãy tưởng tượng bạn lăn mỗi con xúc xắc 6 lần:
- Con xúc xắc đầu tiên cho ra các số 3, 6, 6, 4, 3, 3. Giá trị trung bình là 4,17.
- Con xúc xắc thứ hai cho ra các số 5, 6, 2, 5, 2, 4. Giá trị trung bình là 4,00.
Điều này bây giờ có chứng minh con xúc xắc đầu tiên cho điểm cao hơn con thứ hai không? Có lẽ là không. Một mẫu với các giá trị trung bình chênh lệch không lớn làm cho sự khác biệt dường như vẫn là do các biến ngẫu nhiên. Khi ta tăng số lần lắc xúc xắc, sẽ rất khó để đưa ra câu trả lời thông thường cho câu hỏi – sự khác biệt giữa điểm số là kết quả của sự thay đổi ngẫu nhiên hay thực sự có khả năng con xúc xắc này cho điểm cao hơn con xúc xắc kia?
Significance (mức ý nghĩa) là xác suất, trong đó sự khác biệt mà ta quan sát được giữa các mẫu là do các biến thể ngẫu nhiên. Significance được gọi là cấp độ alpha hoặc đơn giản là “α”. Confidence (mức độ tin cậy), hoặc đơn giản là “c”, là xác suất mà sự khác biệt giữa các mẫu không phải do biến ngẫu nhiên. Nói cách khác, có một sự khác biệt giữa các quần thể (population) cơ bản. Do đó: c = 1 – α.
Bạn có thể đặt “α” ở bất kỳ mức độ nào mình muốn, để cảm thấy tự tin về mức ý nghĩa đã chứng minh. Mức α = 5% (độ tin cậy 95%) được sử dụng thường xuyên, nhưng nếu muốn thực sự chắc chắn rằng bất kỳ sự khác biệt nào đều không phải do biến ngẫu nhiên gây ra, bạn có thể áp dụng mức độ tin cậy cao hơn, sử dụng α = 1% hoặc thậm chí α = 0,1%.
Các thử nghiệm thống kê khác nhau được sử dụng để tính toán độ tin cậy trong các tình huống khác nhau. T-Test được sử dụng để xác định xem số trung bình của hai quần thể có khác nhau không và thử nghiệm F-Test được sử dụng để xác định xem các phương sai có chênh lệch hay không.
Tại sao phải kiểm tra ý nghĩa thống kê?
Khi so sánh những thứ khác nhau, bạn cần sử dụng phương pháp thử nghiệm mức ý nghĩa để xác định xem cái này có tốt hơn cái kia không. Điều này áp dụng cho nhiều lĩnh vực, ví dụ:
- Trong kinh doanh, mọi người cần so sánh các sản phẩm và phương pháp tiếp thị khác nhau.
- Trong thể thao, mọi người cần so sánh các thiết bị, kỹ thuật và đối thủ khác nhau.
- Trong kỹ thuật, mọi người cần so sánh các thiết kế và cài đặt tham số khác nhau.
Nếu bạn muốn kiểm tra xem một thứ gì đó có hoạt động tốt hơn tùy chọn khác không trong bất kỳ lĩnh vực nào, bạn cần kiểm tra ý nghĩa thống kê.
Phân phối t Student là gì?
Phân phối t Student tương tự như phân phối chuẩn (hay còn gọi là Gaussian). Cả hai đều có dạng hình chuông với hầu hết các kết quả gần với giá trị trung bình, nhưng trong một số trường hợp hiếm gặp, kết quả khá xa so với giá trị trung bình theo cả hai hướng, được gọi là đuôi của phân phối.
Hình dạng chính xác của phân phối t Student phụ thuộc vào kích thước mẫu. Đối với các mẫu lớn hơn 30, nó rất giống với phân phối chuẩn. Khi kích thước mẫu giảm, các đuôi sẽ lớn hơn, thể hiện sự không chắc chắn tăng lên từ việc suy luận dựa trên một mẫu nhỏ.
Cách thực hiện T-Test trong Excel
Trước khi bạn có thể áp dụng T-test để xác định xem có sự khác biệt về độ tin cậy mang tính thống kê giữa giá trị trung bình của hai mẫu hay không, trước tiên bạn phải thực hiện F-Test. Điều này là do các tính toán khác nhau được thực hiện cho T-Test tùy thuộc vào việc có sự khác biệt đáng kể giữa các phương sai hay không.
Lưu ý: Bạn sẽ cần add-in Analysis Toolpak được kích hoạt để thực hiện phân tích này.
Kiểm tra và tải add-in Analysis Toolpak
Để kiểm tra và kích hoạt Analysis Toolpak, hãy làm theo các bước sau:
1. Chọn tab FILE > Options.
2. Trong hộp thoại Options, chọn Add-Ins từ các tab ở phía bên trái.
3. Ở dưới cùng của cửa sổ, chọn menu drop-down Manage, sau đó chọn Excel Add-ins, rồi bấm Go.
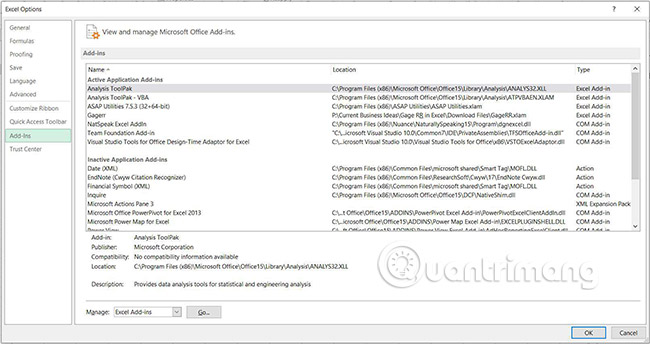
4. Đảm bảo hộp kiểm bên cạnh Analysis Toolpak được chọn, sau đó nhấn vào OK.
5. Analysis Toolpak hiện đang hoạt động. Bạn đã sẵn sàng áp dụng F-Test và T-Test.
Thực hiện F-test và T-test trong Excel
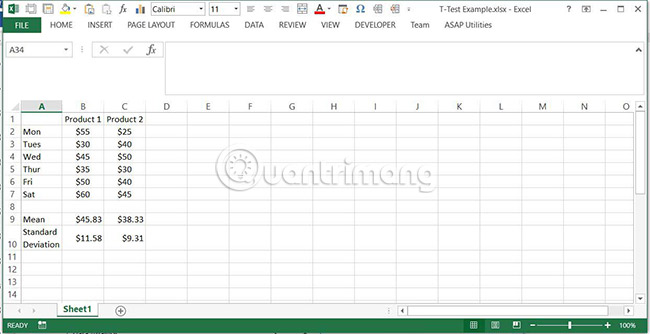
1. Nhập hai bộ dữ liệu vào một bảng tính. Trong trường hợp này, ví dụ đã xem xét việc bán hai sản phẩm trong một tuần. Giá trị doanh số trung bình hàng ngày cho mỗi sản phẩm cũng được tính toán, cùng với độ lệch chuẩn của nó.
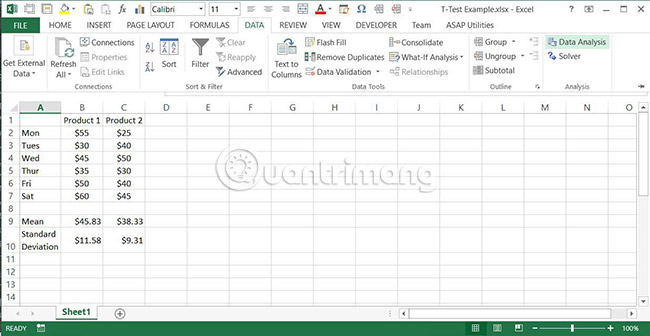
2. Chọn tab Data > Data Analysis.
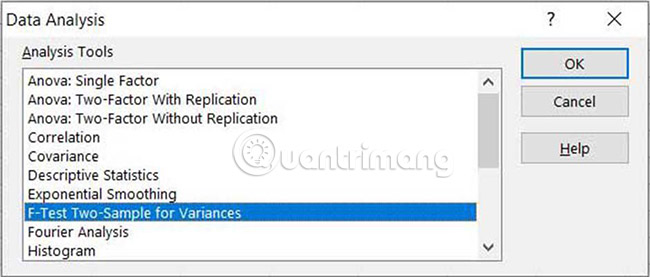
3. Chọn F-Test Two-Sample for Variances từ danh sách, sau đó nhấn OK.
Cảnh báo: F-Test rất nhạy cảm với tính không chuẩn tắc (non-normality). Do đó, sẽ an toàn hơn nếu sử dụng Welch test, nhưng điều này khó thực hiện hơn trong Excel.
4. Chọn Variable 1 Range và Variable 2 Range, đặt Alpha (giá trị 0,05 cho độ tin cậy là 95%), chọn một ô cho góc trên cùng bên trái của đầu ra (đầu ra sẽ lấp đầy 3 cột và 10 hàng. Chọn OK.
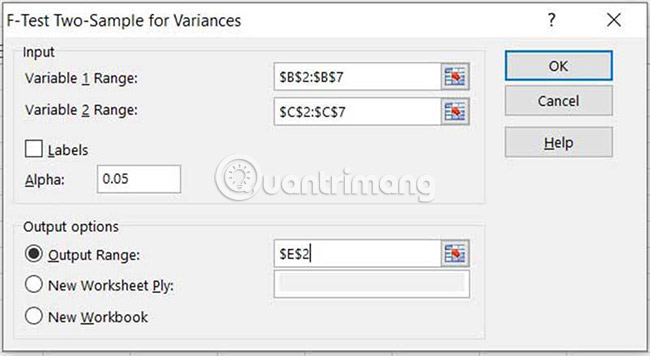
Lưu ý quan trọng: Đối với Variable 1 Range, mẫu với độ lệch chuẩn (hoặc phương sai) lớn nhất phải được chọn.
5. Xem kết quả F-Test để xác định xem có sự khác biệt đáng kể giữa các phương sai hay không. Kết quả cho ba giá trị quan trọng:
- F: Tỷ lệ giữa các phương sai.
- P(F<=f) one-tail: Xác suất mà biến 1 không thực sự có phương sai lớn hơn biến 2. Nếu giá trị này lớn hơn alpha, thường là 0,05, thì không có sự khác biệt đáng kể giữa các phương sai.
- F Critical one-tail: Giá trị của F sẽ được yêu cầu cho P(F<=f)=α. Nếu giá trị này lớn hơn F, điều này cũng cho thấy không có sự khác biệt đáng kể giữa các phương sai.
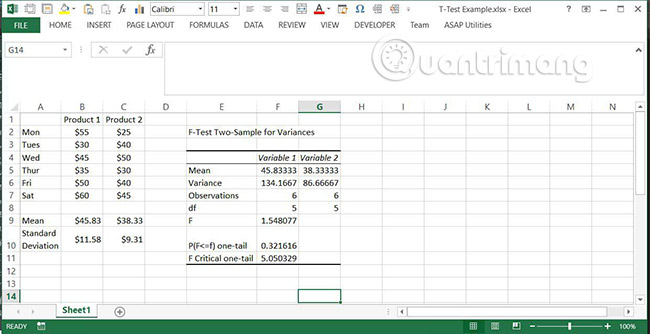
Lưu ý: P(F<=f) cũng có thể được tính bằng hàm FDIST với F và bậc tự do (degrees of freedom) cho mỗi mẫu làm đầu vào của nó. Bậc tự do chỉ đơn giản là số lần quan sát trong một mẫu trừ đi một.
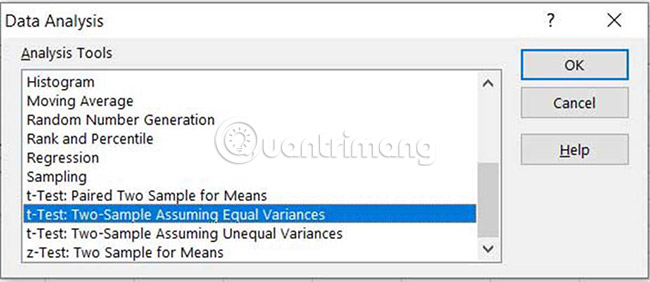
6. Bây giờ, bạn đã biết liệu có sự khác biệt giữa các phương sai hay không và có thể chọn T-Test phù hợp. Chọn tab Data > Data Analysis, sau đó chọn t-Test: Two-Sample Assuming Equal Variances hoặc t-Test: Two-Sample Assuming Unequal Variances.
7. Bất kể bạn chọn tùy chọn nào trong bước trước, bạn sẽ thấy cùng một hộp thoại để nhập chi tiết phân tích. Để bắt đầu, chọn phạm vi chứa các mẫu cho Variable 1 Range và Variable 2 Range.
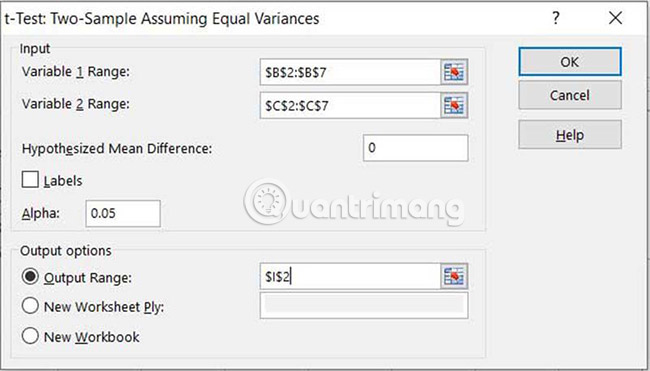
8. Giả sử bạn muốn kiểm tra để chắc chắn không có sự khác biệt giữa các giá trị trung bình, hãy đặt Hypothesized Mean Difference thành 0.
9. Đặt mức ý nghĩa Alpha (0,05 tương đương với độ tin cậy 95%) và chọn một ô cho góc trên cùng bên trái của đầu ra (đầu ra sẽ lấp đầy 3 cột và 14 hàng). Chọn OK.
10. Xem lại kết quả để quyết định xem có sự khác biệt đáng kể giữa các giá trị trung bình không.
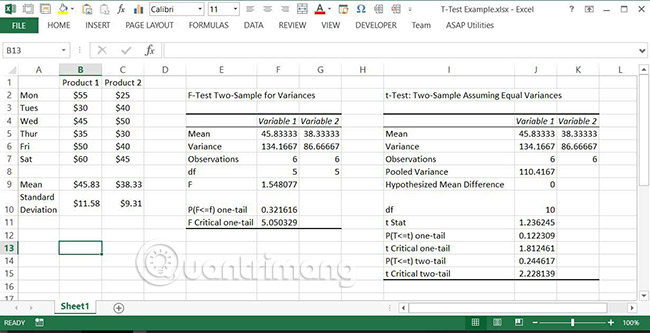
Lưu ý: Giống như với F-Test, nếu giá trị p, trong trường hợp này là P(T<=t), lớn hơn alpha, thì không có sự khác biệt đáng kể. Tuy nhiên, trong trường hợp này, có hai giá trị p được đưa ra, một cho thử nghiệm một đuôi và cái còn lại cho thử nghiệm hai đuôi. Trường hợp này sử dụng giá trị hai đuôi vì một trong hai biến có giá trị trung bình lớn hơn sẽ là một sự khác biệt đáng kể.
?DienDan.Edu.Vn cám ơn bạn đã quan tâm và rất vui vì bài viết đã đem lại thông tin hữu ích cho bạn. https://diendan.edu.vn/

DienDan.Edu.Vn Cám ơn bạn đã quan tâm và rất vui vì bài viết đã đem lại thông tin hữu ích cho bạn.DienDan.Edu.Vn! là một website với tiêu chí chia sẻ thông tin,... Bạn có thể nhận xét, bổ sung hay yêu cầu hướng dẫn liên quan đến bài viết. Vậy nên đề nghị các bạn cũng không quảng cáo trong comment này ngoại trừ trong chính phần tên của bạn.Cám ơn.






